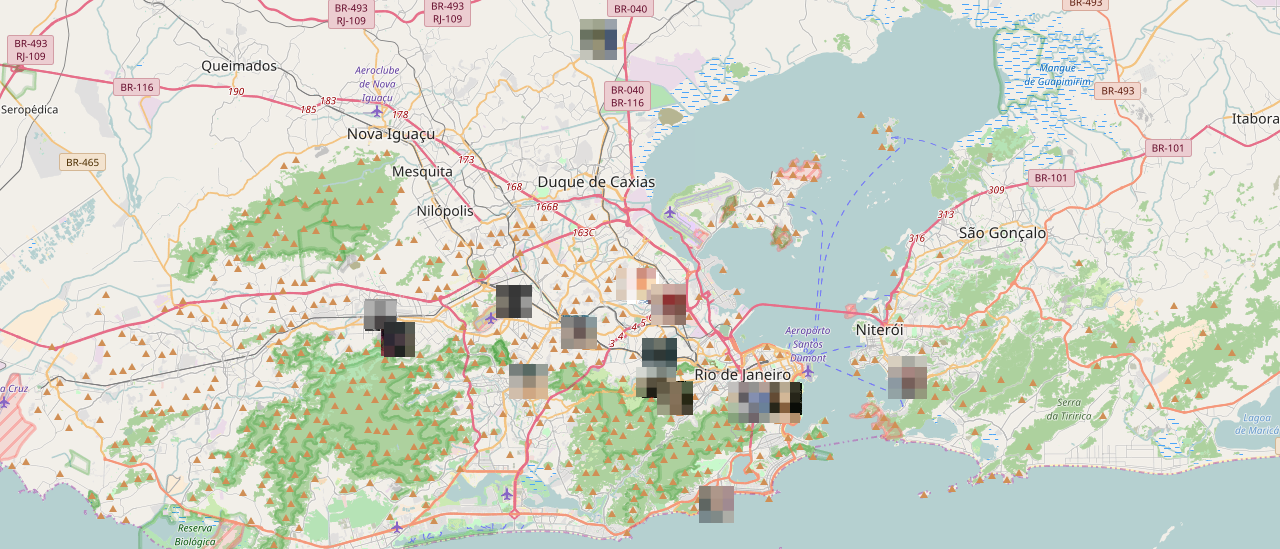
Como eu consegui descobrir a localização dos meus matches no Tinder (ou quase)
Esse post é bem antigo. Muita coisa pode estar incorreta devido a novidades que aconteceram desde então, ou porque meu entendimento na época não era tão claro.
Eu já havia percebido uma possível vulnerabilidade de segurança no Tinder havia um tempo. Ele permite que você saiba as distâncias em que outros usuários se encontram em relação a você. Embora pareçam inofensivas, informações sobre distâncias, somadas a um pouco de perspicácia, permitem descobrir a posição exata de qualquer pessoa. Para isso, usa-se uma técnica chamada trilateração. Evidentemente, não fui o primeiro a pensar neste problema: a técnica é usada no GPS, por exemplo, e também já foi empregada com precisamente a mesma finalidade que a minha pela Include Security.
De todo modo, precisava de um tema para o projeto da disciplina de Cálculo Numérico este semestre e essa ideia parecia viável (dadas as minhas limitações de tempo) e suficientemente divertida, e cá estamos. Este artigo vai explicar como defini matematicamente o problema, utilizei programação para implementar um protótipo e quais conclusões obtive, além de uma visualização como a do header acima.
A ideia
A técnica é baseada em geometria elementar. Consideremos, inicialmente, que a terra é perfeitamente plana. Imagine que um contato está a uma distância de 5 quilômetros de você, que se encontra no ponto A. O conjunto de possíveis localizações dele determina uma circunferência de 5km de raio. Agora você vai para uma segunda posição B e verifica novamente a distância dita pelo aplicativo, que agora é de 7km. Se o problema for bem posto, tipicamente a busca será reduzida para duas possibilidades:
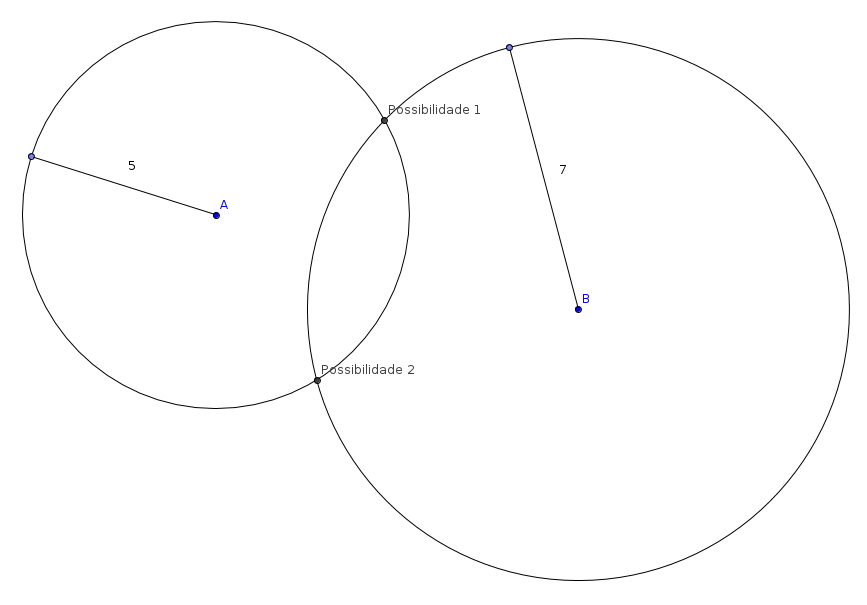
Movendo-se para uma terceira localização, basta comparar a distância fornecida pelo aplicativo com a distância aos dois pontos que restaram, e será possível eliminar o caso falso. Pronto, localização descoberta! Claro, você deve ter algumas objeções agora:
- A distância fornecida pelo Tinder é arredondada, não é a distância real. No aplicativo não, mas a Pynder, API pirata do Tinder para Python, permite pegar a distância com precisão dupla. Se essa distância for a correta, estamos bem.
- A premissa de que a pessoa não se move enquanto mudamos de posição é muito forte! De fato, mas a verdade é que esse deslocamento nunca será feito na prática. A API nos permite definir nossa latitude e longitude de forma arbitrária, sem precisarmos ter nos movido de fato.
- A terra não é plana, Luiz. Claro, tanto que irei modelar a Terra como uma esfera ao longo do texto. Apesar disso, em muitos aspectos a geometria da superfície da esfera é análoga a do plano, quando os conceitos envolvidos são corretamente correspondidos, e essa intuição é de muito uso.
A formulação matemática do problema
A terra será modelada como uma esfera de raio 6378.008km, que é o valor calculado para o raio médio da Terra a partir do elipsoide WGS-84. A precisão obtida será, obviamente, menor que aquela que eu teria caso usasse o próprio WGS-84, mas ao menos para esse projeto o trade-off entre 0.5% de precisão e o grande ganho em simplicidade das contas compensa. A posição de um ponto na superfície dessa esfera é especificada por uma latitude e uma longitude, costumeiramente representados pelas letras $\phi$ e $\lambda$, respectivamente.
Neste caso, o ângulo central $\Delta\sigma$ entre os pontos $\phi_1, \lambda_1$ e $\phi_2, \lambda_2$ é dado pela fórmula
\[\Delta\sigma((\phi_1, \lambda_1), (\phi_2, \lambda_2))=\arccos\bigl(\sin\phi_1\cdot\sin\phi_2+\cos\phi_1\cdot\cos\phi_2\cdot\cos(\Delta\lambda)\bigr)\]Para obter a distância de fato, basta multiplicar este ângulo pelo raio $r_T$ da Terra. Medições são feitas em três pontos $A = (\phi_A, \lambda_A)$, $B = (\phi_B, \lambda_B)$ e $C = (\phi_C, \lambda_C)$ arbitrários. A única restrição é que os três pontos não sejam colineares, ou melhor, que não estejam na mesma geodésia, o análogo ao conceito de reta quanto falamos da superfície da Terra. Isso deve ser observado porque, neste caso, o terceiro ponto é inútil para distinguir entre a posição real a posição falsa, pois as distâncias observadas serão as mesmas.
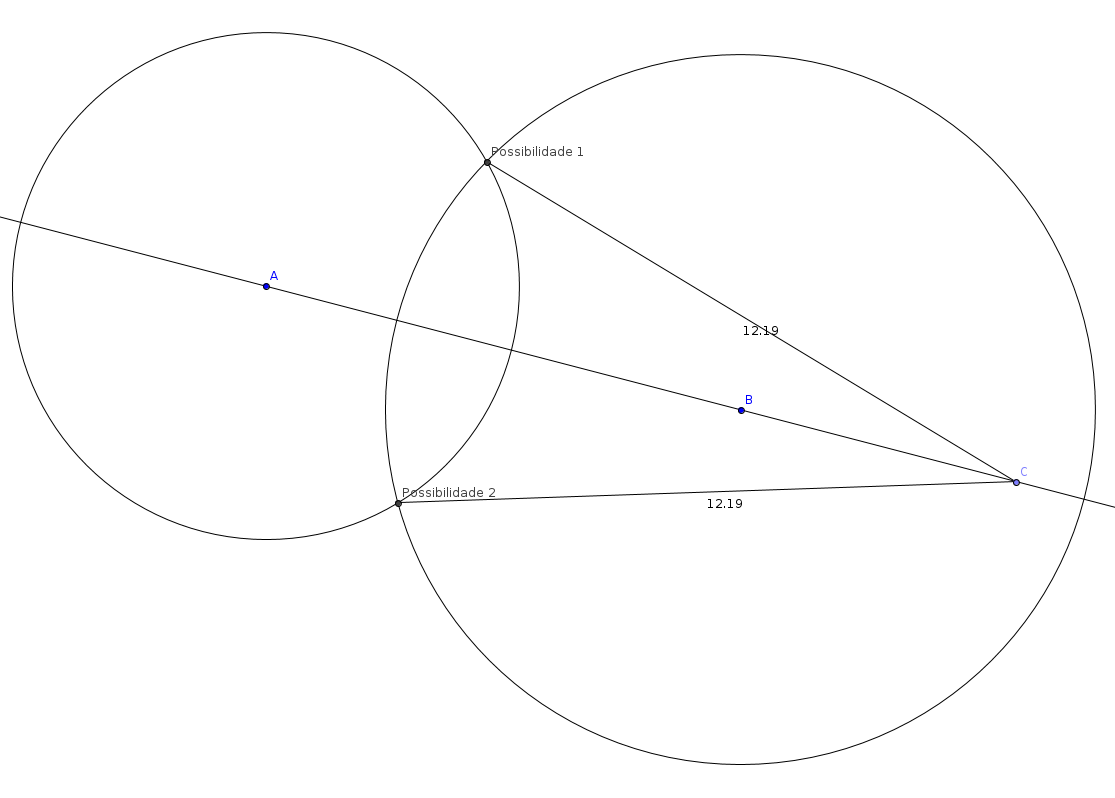
O objetivo é descobrir qual o ponto $P = (\phi^{\ast}, \lambda^{\ast})$ com medições de distância $d_A = r_T\Delta\sigma(P, A)$, $d_B = r_T\Delta\sigma(P, B)$ e $d_C = r_T\Delta\sigma(P, C)$. Definindo a função $F(X) = (r_T\Delta\sigma(X, A) - d_A, r_T\Delta\sigma(X, B) - d_B)$, vê-se claramente que o ponto que estamos procurando é uma raiz de F. Portanto, podemos nos concentrar em encontrar as soluções $S = \{P_1, P_2\}$ da equação $F(X) = 0$.
Por último, devemos usar o terceiro ponto para fazer uma escolha entre as duas opções que restaram. A localização final é dada por $argmin_{P \in S} {| r_T\Delta\sigma(P, C) - d_C|}$. Note que, em termos estritamente matemáticos, a solução final deveria ser o ponto $P_1$ ou $P_2$ que satisfizesse $r_T\Delta\sigma(P, C) = d_C$ de forma exata, mas admitimos uma imprecisão devido aos métodos numéricos envolvidos no processo.
A coleta dos dados
Para a coleta dos dados eu usei a API Pynder. O script é bastante simples e não precisa de muitos comentários. Em linhas gerais, capturo as informações de nome, foto, última hora em que seu posicionamento foi atualizado, e faço três medições a partir de pontos mais ou menos arbitrários. No fim, jogo tudo isso para a saída padrão como JSON.
# py/get_coords.py
import pynder
import json
# lê id e senha da entrada padrão
facebook_id = input()
facebook_token = input()
# loga
session = pynder.Session(facebook_id = facebook_id,
facebook_token = facebook_token)
# pega o posicionamento atual
lat = session.profile._data['pos']['lat']
lng = session.profile._data['pos']['lon']
data = dict()
data['pos1'] = [lat, lng]
data['pos2'] = [lat - .25, lng - .25]
data['pos3'] = [lat - .25, lng]
data['matches'] = []
# varre os matches coletando infos e distâncias ao ponto atual
for match in session.matches():
photos = match.user.get_photos()
picture = photos[0] if (len(photos) > 0) else "egg.png"
data['matches'].append({
'name': match.user.name,
'picture': picture,
'last_online': match.user.ping_time,
'dist1': match.user.distance_km
})
# segunda medição: atualiza a posição e pega as novas distâncias
session.update_location(lat - .25, lng - .25)
i = 0
for match in session.matches():
data['matches'][i]['dist2'] = match.user.distance_km
i += 1
# terceira medição: atualiza a posição e pega as novas distâncias
session.update_location(lat - .25, lng)
i = 0
for match in session.matches():
data['matches'][i]['dist3'] = match.user.distance_km
i += 1
# joga os dados coletados na saída padrão
print(json.dumps(data))
A solução numérica
Queremos encontrar a raiz de uma função $F$ que foi definida de um modo bastante complicado. Parece trabalhosa (provavelmente impossível) de resolver analiticamente, isto é, utilizando somente manipulações algébricas. No entanto, é possível encontrar aproximações para as raízes usando métodos numéricos. Neste caso, podemos usar uma versão do método de Newton.
A ideia é simples. Damos um chute inicial $X_0$ de onde a raiz deve estar e, chegando lá, usamos informações sobre a função e suas derivadas parciais para estimar onde a raiz dessa função deveria estar localizada caso a função variasse de um modo linear. Claro, a função não é realmente linear, mas ao menos devemos ficar mais perto da raiz do que estávamos antes. Com isso, chegamos ao um novo ponto $X_1$. Repetimos esse processo até que nos demos por satisfeitos.
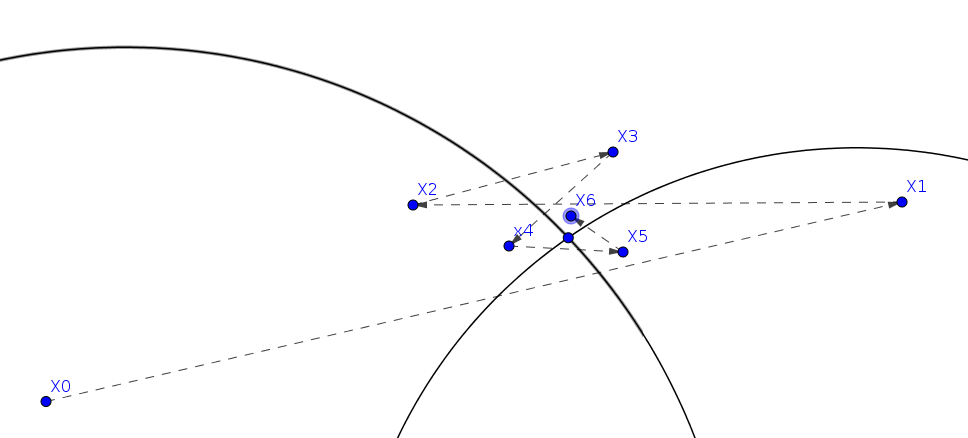
Matematicamente, a relação entre um chute e o próximo é expressa por $X_{n+1} = X_n - J_F (X_n)^{-1} F(X_n)$,
onde $J_F$ é a jacobiana de $F$. Essa relação sugere claramente o uso de um loop. No código
abaixo, eu defino dist, que é essencialmente a função $F$ definida anteriormente, sem a subtração
das distâncias medidas. A partir dela, crio uma função que gera as funções $F$ para
cada contato em que estamos interessados, que nada mais são que deslocamentos
da dist original. Defino também a jacobiana e a função para calcular a raiz de F
usando o método de Newton. Programei o método de Newton de modo a parar quando
já estiver dando passos menores que $10^{-12}$ ou já tiver dado mais de 20000
passos.
# R/newton.R
dist = function(P, A, B) {
lat = radians(P[1])
lng = radians(P[2])
lat_i = radians(c(A[1], B[1]))
lng_i = radians(c(A[2], B[2]))
cosines = sin(lat_i)*sin(lat) + cos(lat_i)*cos(lat)*cos(lng - lng_i)
EARTH_RADIUS * acos(cosines)
}
jacobianOfDist = function(P, A, B) {
lat = radians(P[1])
lng = radians(P[2])
lat_i = radians(c(A[1], B[1]))
lng_i = radians(c(A[2], B[2]))
cosines = sin(lat_i)*sin(lat) + cos(lat_i)*cos(lat)*cos(lng - lng_i)
dlat = EARTH_RADIUS * (-sin(lat_i)*cos(lat) + cos(lat_i)*sin(lat)*cos(lng - lng_i)) / sqrt(1 - cosines*cosines)
dlng = EARTH_RADIUS * cos(lat_i)*cos(lat)*sin(lng - lng_i) / sqrt(1 - cosines*cosines)
cbind(dlat, dlng)
}
getDistFunction = function(dist0, A, B) {
dist0
function(P) {
dist(P, A, B) - dist0
}
}
getJacobianFunction = function(A, B) {
function(P) {
jacobianOfDist(P, A, B)
}
}
newton = function(f, x0, j, epsilon = 1E-12, max = 20000) {
oldGuess = x0
for (i in 1:max) {
guess = oldGuess + solve(j(oldGuess), -f(oldGuess))
if (norm(guess - oldGuess, type = "2") < epsilon)
break
oldGuess = guess
}
guess
}
Uma questão ainda ficou em aberto: precisamos das duas raízes, mas o método de Newton só encontra uma delas. Pra ser mais preciso, a raiz que o método de Newton encontra depende exclusivamente do chute inicial que damos. O problema é que, no caso geral, é muito difícil identificar para qual das raízes o sistema vai convergir dependendo do chute inicial. De primeira pensei em dar chutes iniciais aleatórios. Ora, a estrutura do problema parece bastante simétrica, fifty-fifty e seria improvável que, partindo de pontos iniciais aleatórios, eu chegasse sempre na mesma raiz. Uma hora o método vai ter que me dar as duas raízes!
Funcionou, mas resolvi pensar um pouco mais sobre a simetria do problema. Consegui provar, por exemplo, que as duas raízes são reflexões uma da outra em torno da geodésia que liga A a B. Uma intuição que tive é que, se dermos chutes iniciais refletidos em torno dessa geodésia, cada chute inicial deveria resultar numa raiz diferente. Não consegui provar esse fato, mas a intuição pareceu funcionar na prática. Se $A = (\phi_A, \lambda_A)$ e $B = (\phi_B, \lambda_B)$, dou chutes iniciais em $(\phi_A, \lambda_B)$ e $(\phi_B, \lambda_A)$. Se a terra fosse plana, estes quatro pontos formariam um quadrado e os chutes iniciais seriam reflexões um do outro. A terra não é plana, mas a figura formada fica muito perto de ser um quadrado quando os pontos A e B são escolhidos suficientemente próximos. Na prática, esses chutes funcionaram e consegui obter as duas raízes deste modo.
O resultado final
Para visualizar os resultados, criei um aplicativo Shiny usando o pacote Leaflet,
que permite a criação de mapas interativos. Os cálculos dos pontos são feitos
no arquivo global.R utilizando as ideias descritas acima:
# global.R
library(shiny)
library(shinydashboard)
library(purrr)
library(jsonlite)
library(leaflet)
library(glue)
source("R/newton.R", encoding = "UTF-8")
EARTH_RADIUS = 6371.008
data = fromJSON("out.json")
matches = data$matches
pos1 = data$pos1
pos2 = data$pos2
pos3 = data$pos3
# gera as funções objetivo e a jacobiana
funcs = map(1:n, ~ getDistFunction(c(matches$dist1[.], matches$dist2[.]), pos1, pos2))
jacobian = getJacobianFunction(pos1, pos2)
# calcula numericamente as duas possíveis soluções
solution1 = map(funcs, newton, j = jacobian, x0 = c(pos1[1], pos2[2]))
solution2 = map(funcs, newton, j = jacobian, x0 = c(pos2[1], pos1[2]))
decide = function(p1, p2, d, p3) {
distances = dist(p3, p1, p2)
if (abs(distances[1] - d) < abs(distances[2] - d))
p1
else
p2
}
definiteSolution = pmap(list(solution1, solution2, matches$dist3), decide, p3 = pos3)
matches$lat = map_dbl(1:n, ~ definiteSolution[[.]][1])
matches$lng = map_dbl(1:n, ~ definiteSolution[[.]][2])
O código dos outros arquivos não é muito interessante.
# ui.R
dashboardPage(
dashboardHeader(title = "Match Locator"),
dashboardSidebar(disable = TRUE),
dashboardBody(
fluidRow(
column(width = 12,
box(title = "Mapa", width = NULL,
leafletOutput("mapa", height = 600),
solidHeader = TRUE, status = "primary"
)
)
)
)
)
# server.R
function(input, output, session) {
output$mapa = renderLeaflet({
leaflet() %>%
addTiles() %>%
addMarkers(lat = matches$lat, lng = matches$lng, popup = matches$name,
icon = icons(matches$picture, iconWidth = 32, iconHeight = 32))
})
}
O importante é que isso me gerou a seguinte visualização no mapa:
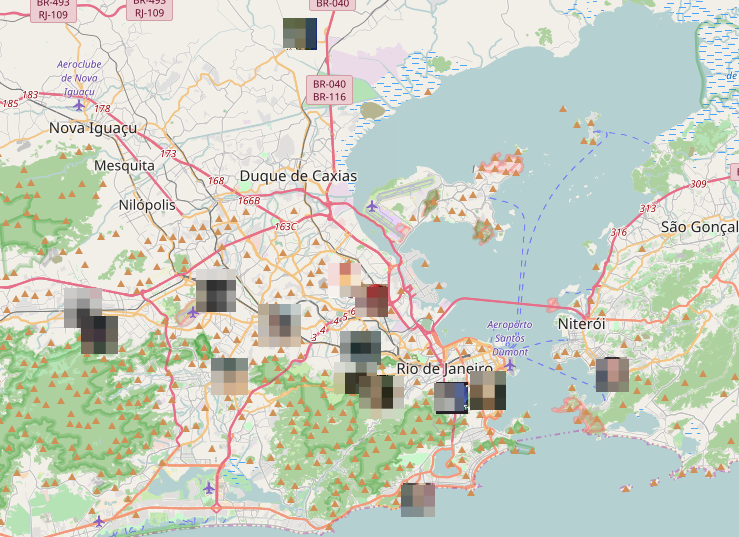
Aparentemente as posições encontradas fazem sentido. Não tem ninguém dentro da floresta da tijuca ou da Baía de Guanabara, por exemplo. Quando dei zoom maior, no entanto, vi que havia uma moça usando o Tinder enquanto morria afogada… ou então o método que falhou mesmo.

Fui investigar a questão mais um pouco e montei uma tabela com as diferenças entre as distâncias medidas pelo Tinder e as distâncias dos pontos que obtive em relação aos pontos A, B e C onde das medições foram feitas. Se tudo estivesse correto, esta diferença deveria ser muito próxima de zero. Isso aconteceu com as distâncias até A e B, afinal, foi para isso que usei o método de Newton. No entanto, quando comparados com o ponto C, a distância real do ponto encontrado e a distância dada pelo Tinder diferiam, na média, em 624m. Erros desta magnitude não deveriam acontecer mesmo levando em consideração que estou aproximando a Terra por uma esfera e não por um elipsoide.
Não tenho como confirmar minhas suspeitas, mas acredito que o Tinder fornece as distâncias reais somadas a um ruído aleatório de magnitude menor que 1km. Esse ruído muda muito pouco a vida do usuário comum, que afinal lê as distâncias arredondadas, mas é suficiente para impedir que alguém com acesso a API possa usá-la para localizar alguém. Essa é uma ideia que me parece até mais inteligente que dar acesso ao valor arredondado da distância pela API, como faziam antes, pois neste caso ainda seria possível conseguir uma boa estimativa da localização do usuário usando uma quantidade grande de medições. De todo modo, os resultados que obtive parecem precisos o suficiente ao menos para ter uma ideia do bairro onde os seus matches estão.
Conclusão: Parece que o Tinder já tinha ouvido a Include Security e bolou um mecanismo inteligente que elimina essa brecha.
Conclusão atualizada (29/08/2018): Na verdade a equipe do Tinder bolou uma solução ainda melhor do que a que havia comentado antes. Na época, suspeitava que a posição real fosse somada a um ruido aleatório. Isso preveniria ataques que exploram a descontinuidade dos arredonamentos, mas ainda deixaria suscetível à Lei dos Grandes Números. A solução implementada contorna isso. Ver aqui.
Try it yourself!
Caso você tenha algum conhecimento de R e Python, você pode testar o protótipo
que desenvolvi, cujo código está disponível neste repositório. Primeiro,
você vai precisar usar o script py/auth.py para pegar o auth token do facebook.
Pegue também o seu id do Facebook nesse site. Crie um arquivo texto
contendo o id na primeira linha e o auth token na segunda. Depois, rode o
seguinte comando:
python py/get_coords.py < arquivo.txt > out.json
Isso bastará para gerar o arquivo JSON contendo as informações do Tinder. Por
último, basta rodar o aplicativo Shiny e ver os resultados. O uso do RStudio
é bem conveniente para isso. Para rodar tudo, você precisará dos pacotes RoboBrowser, Pynder e lxml no Python
e shiny, shinydashboard, purrr, jsonlite e leaflet no R.